swddude is very young pre-alpha software. Caveat downloader.

swddude is a collection of simple tools for programming and using ARM Cortex microcontrollers, such as the Cortex-M0 and M3, using the SWD protocol.

Subdiv is the beginings of a subdivision surface renderer.

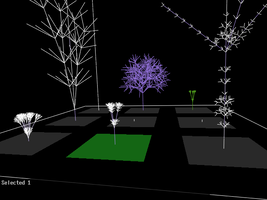
This is a user driven Genetic Algorithm plant evolution program.

Puzzle is my implimentation of the game that Rus turned me on to.

Hey, who dosn't like a fun particle simulator?

Puddle is an OpenGL wave equation simulation.

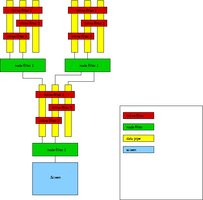
Morbit is an architecture for efficiently building arbitrary function tree's. I use it to generate most of the fractals that I play with and its an ongoing project.

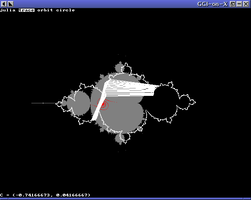
A utility for demonstrating the math for Julia fractals.

These are samples from an old fractal renderer I wrote.

1 post.